Регистрация
daniil326
15.10.2020 11:21
Математика
Есть ответ 👍

(n-1)!/(n-3)!≤6
Определите количество целых решений ​

263
275
Посмотреть ответы 3

Ответы на вопрос:

Hol0Ze5
Hol0Ze5
4,6(57 оценок)

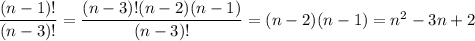
\dfrac{(n-1)!}{(n-3)!}=\dfrac{(n-3)!(n-2)(n-1)}{(n-3)!}=(n-2)(n-1)=n^2-3n+2

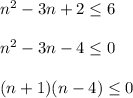
n^2-3n+2\leq 6\\ \\ n^2-3n-4\leq 0\\ \\ (n+1)(n-4)\leq 0

n \in [-1;4]

С учетом того, что 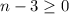n-3\geq0 откуда 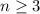n\geq3 ответом неравенства есть n \in [3;4] откуда целые решения это 3 и 4.

verenikinaulia
verenikinaulia
4,4(43 оценок)

2

Пошаговое объяснение:

Для начала заметим, что аргумент факториала есть неотрицательное целое число, поэтому ОДЗ: n≥3, n ∈ Z.

Числитель дроби можно представить в виде: (n-1)! = (n-1)(n-2)·(n-3)!

Так как факториал не может обратиться в 0, то можно безболезненно сократить числитель и знаменатель на (n-3)!

(n-1)(n-2)≤6;

n²-3n+2≤6;

n²-3n-4≤0;

(n+1)(n-4)≤0;

Находим решение этого неравенства, например, методом интервалов: -1≤n≤4;

C учетом ОДЗ: 3≤n≤4.

Значит, целых решений всего два: 3 и 4

asyavish15oy8la6
asyavish15oy8la6
4,6(10 оценок)
8/10,4/7,3/10,7/10.

Популярно: Математика