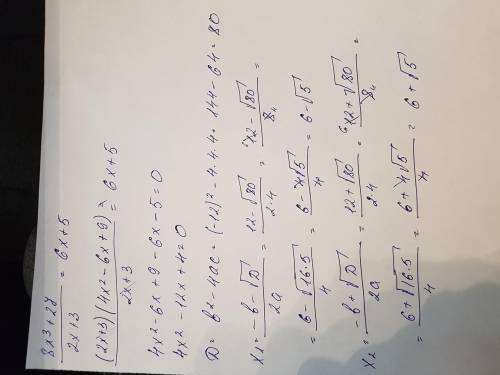Зная, что ряд ^{n+1}}{n} =ln2) , найти сумма ряда, полученного путем перестановки его членов
, найти сумма ряда, полученного путем перестановки его членов
[tex]1+\frac{1}{3} -\frac{1}{2}+\frac{1}{5} +\frac{1}{7} -\frac{1}{4}+/tex]
Ответы на вопрос:
пример
последовательность монотонно стремится к нулю, поэтому по признаку лейбница ряд сходится. найдем
выпишу формулу пусть . эйлер получил асимптотическое выражение для суммы первых n членов ряда:
где значение
следовательно,
- последовательность частичных сумм данного ряда.
это мы показали что тот ряд равен ln 2. теперь перейдем к нашем .
[tex]1+\dfrac{1}{3}+\dfrac{1}{5}++\dfrac{1}{2a-1}-\dfrac{1}{2}-\dfrac{1}{4}--\dfrac{1}{2b}+\dfrac{1}{2a+1}+\dfrac{1}{2a+3}+\\ \\ \\ ++\dfrac{1}{4b-1}-/tex]
в силу примера, что мы показали в начале, мы получим
[tex]1+\dfrac{1}{3}+\dfrac{1}{5}++\dfrac{1}{2a-1}-\bigg(\dfrac{1}{2}+\dfrac{1}{4}++\dfrac{1}{2b}\bigg)+\\ \\ \\ +\bigg(\dfrac{1}{2a+1}+\dfrac{1}{2a+3}++\dfrac{1}{4b-1}\bigg)-/tex]
первые две скобки - ряда сходятся, теперь нужно показать что последнее тоже сходится.
Популярно: Алгебра
-
Sin^2 x-3sinxcosx+cos2x=-1 (10 класс)...
 AnnaKhusainova24.12.2021 04:17
AnnaKhusainova24.12.2021 04:17 -
Поезд,двигаясь равномерно со скоростью 150км/ч ,проезжает мимо столба за...
 Zikeev200727.01.2023 06:24
Zikeev200727.01.2023 06:24 -
Периметр прямоугольника равен 20 см. найдите его стороны,если известно,что...
 Elaria101.05.2022 16:46
Elaria101.05.2022 16:46 -
2. розв’яжіть рівняння 7х2 – 28 = 0 а) 0; б) -2 і 2; в) 0 і 2; г) 2...
 dibalabagdasar25.11.2022 20:25
dibalabagdasar25.11.2022 20:25 -
Как расположены графики функций у -15х-14 и у -15х+12...
 Usoll15.02.2020 18:32
Usoll15.02.2020 18:32 -
Решите систему уравнений: 3(х+у)+1=х+4у; 7-2(х-у)=х-8у....
 NeZnAYkA0000000001.05.2023 08:49
NeZnAYkA0000000001.05.2023 08:49 -
100 бaллoв! oчень задание в закрепe (14.14)...
 1nVictUS16.05.2021 00:29
1nVictUS16.05.2021 00:29 -
Нужно Решить номер 4 под пунктом а) и б)...
 howl11101.03.2022 19:40
howl11101.03.2022 19:40 -
Внесите множитель под знак корня 6√5...
 Крутая19502304.04.2020 06:12
Крутая19502304.04.2020 06:12 -
Установите равносильны ли неравенства x-7/x^2+1 0 и (7-x)*(х+3) 0...
 Alicewonderr05.03.2021 09:13
Alicewonderr05.03.2021 09:13