Доказать, что если четное число n не делится на 3 и 4, то n5 - 5n3 + 4n делится на 1440 кто знает правильный ответ пишите быстрее мне ужасно надо.
172
180
Ответы на вопрос:
1440=2*2*2*2*2*3*3*5 =(n-2)(n-1)n(n+1)(n+2) поищем множители числа 1440.. пять двоек: n - четно, но не делится на 4 (значит с него одна 2 есть) n-1 и n+1 -нечетные n-2 и n+2 четные, и в отличии от n делятся на 4=2*2, значит с них по 2 двойки всего получили 5 двоек, что и надо было две тройки: n не делится на 3, значит на 3 делится либо n+1 и n-2, либо n+2 и n-1итак получили, что два множителя на 3 делятся .. то есть 2 троечки в пройзведение пятерочка: у нас произведение 5 последовательных чисел, одно из них точно делится на 5 итог: все делители числа 1440 присутствуют в заданном числе, при заданных условиял, значит 1440 является делителем данного числа чтд
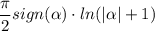
Пошаговое объяснение:
На мн-ве 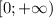 подынтегральная функция, очевидно, определена везде, кроме точки x=0.
подынтегральная функция, очевидно, определена везде, кроме точки x=0.
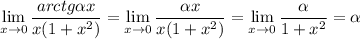
А тогда, если доопределить подынтегральную функцию в нуле значением 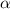 , она станет непрерывной по x на промежутке
, она станет непрерывной по x на промежутке 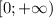 . При этом, очевидно, на значение интеграла такое доопределение не влияет.
. При этом, очевидно, на значение интеграла такое доопределение не влияет.
По 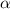 подынтегральная функция, очевидно, непрерывна.
подынтегральная функция, очевидно, непрерывна.
А тогда, согласно теореме о дифференцировании по параметру, получим:
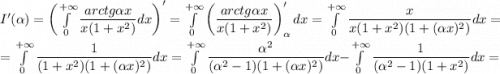
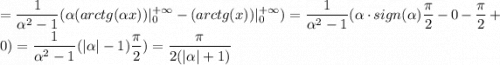
Тогда
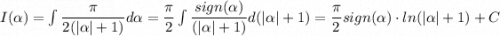
Очевидно для начального условия взять 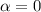 :
:
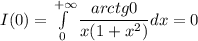
А тогда 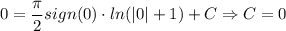
Популярно: Математика
-
Скажите как решать 4б класса автор а.л. чекин...
 lapshinauly20.12.2021 12:49
lapshinauly20.12.2021 12:49 -
Вквадрате 9 ёжиков разделить начертив два квадрата...
 knarik8805.05.2022 18:20
knarik8805.05.2022 18:20 -
Первого дня художню вистовку видвидали 120 осиб другогоу 3 рази бильше...
 Саляриум14.06.2021 11:11
Саляриум14.06.2021 11:11 -
Какая фамилия была у офицера возглавлявших команды зажигательных судов?...
 strelkina4226.03.2020 05:38
strelkina4226.03.2020 05:38 -
:магазин закупил книги по оптовой цене 100 р. и стал продавать с наценкой...
 ulyanasims27.09.2022 07:48
ulyanasims27.09.2022 07:48 -
Городниця на ринок 420 кг цибулі і 300 кг. часнику в однакових ящиках....
 sashamay201617.01.2021 12:04
sashamay201617.01.2021 12:04 -
Периметр прямоугольника равен 44 целым и одна вторая а ширина 10 целых...
 2K9928.07.2022 06:21
2K9928.07.2022 06:21 -
Рита и галя играют в слова.лида записала на 18 слов больше,чем рита,и...
 yyeyheh06.08.2020 06:07
yyeyheh06.08.2020 06:07 -
Занятие кружка началось в 9 ч 20 мин и продолжалось 45 мин. в котором...
 OlgaNazarenko12320.01.2023 04:13
OlgaNazarenko12320.01.2023 04:13 -
Запишите период бесконечной десятичной периодической дроби в скобках...
 tawawma17.04.2022 13:31
tawawma17.04.2022 13:31
