Регистрация
ngjjndnd
20.12.2022 13:40
Математика
Есть ответ 👍

Доказать неравенство, если a>0, b>0, c>0
(Довести нерівність, якщо a>0, b>0, c>o)

190
420
Посмотреть ответы 2

Ответы на вопрос:

20Lorans03
20Lorans03
4,7(57 оценок)

Нужно применить метод ранее доказанного неравенства:

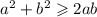
{a}^{2} + {b}^{2} \geqslant 2ab

Из нее следует:

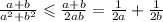
\frac{a + b}{ {a}^{2} + {b}^{2} } \leqslant \frac{a + b}{2ab} = \frac{1}{2a} + \frac{1}{2b}

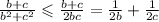
\frac{b + c}{ {b}^{2} + {c}^{2} } \leqslant \frac{b + c}{2bc} = \frac{1}{2b} + \frac{1}{2c}

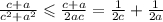
\frac{c + a}{ {c}^{2} + {a}^{2} } \leqslant \frac{c + a}{2ac} = \frac{1}{2c} + \frac{1}{2a}

Теперь по свойству почленного прибавления неравенств, получим :

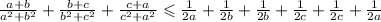
\frac{a + b}{{a}^{2} + {b}^{2} } + \frac{b + c}{ {b}^{2} + {c}^{2} } + \frac{c + a}{ {c}^{2} + {a}^{2} } \leqslant \frac{1}{2a} + \frac{1}{2b} + \frac{1}{2b} + \frac{1}{2c} + \frac{1}{2c} + \frac{1}{2a}

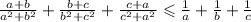
\frac{a + b}{{a}^{2} + {b}^{2} } + \frac{b + c}{ {b}^{2} + {c}^{2} } + \frac{c + a}{ {c}^{2} + {a}^{2} } \leqslant \frac{1}{a} + \frac{1}{b} + \frac{1}{c}

Доказано

sevsdasdaddd
sevsdasdaddd
4,7(52 оценок)

ответ:

0,96

пошаговое объяснение: 150-6=144

144/150= 0,96

Популярно: Математика