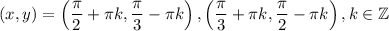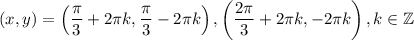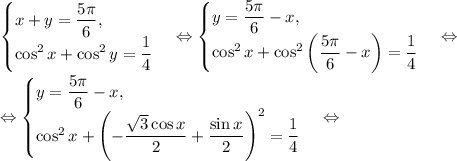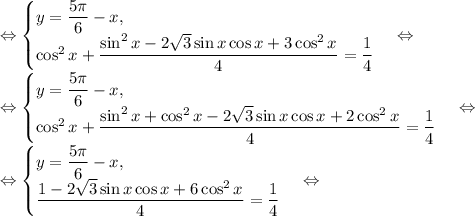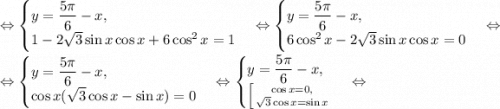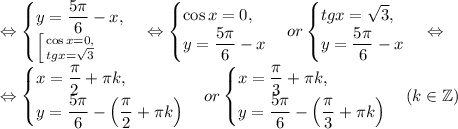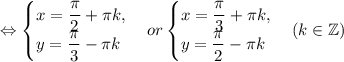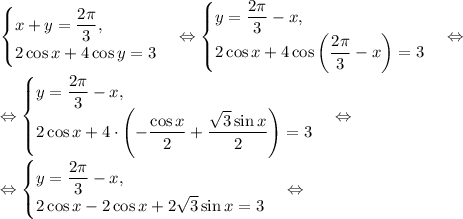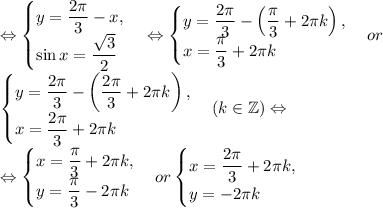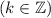алгебра: решите системы тригонометрических уравнений: {x+y=5/6π, cos^2x+cos^2y=1/4; {x+y=2/3π, 2cosx+4cosy=3:
157
401
Ответы на вопрос:
(2П/3+2пk; 2Пl) k=-l k,l ∈Z
(П/3+2Пk; П/3+2Пl);
Объяснение:
x+y=П-П/3 x=П-(П/3+y)
2cosx+4cosy=3
2cos(П-(П/3+y))+4cosy=3
-2cos(П/3+y)+4cosy=3
-cosy+√3siny+4cosy=3
√3cosy+siny=√3 :2
cos(y-П/6)=√3/2
y-П/6=П/6+2Пk y=П/3+2Пk x=П-(П/3+П/3+2Пk)
y-П/6=-П/6+2Пk y=2Пk x=П-(П/3+2Пk)=2П/3-2пk

Популярно: Алгебра
-
Решить уравнение 4^x-14*2^x-32=0 решить неравенства 1) 2^2x-9 1 2) (1/3)^2x-6(1/3)^x-27...
 alnoskoff04.02.2023 08:14
alnoskoff04.02.2023 08:14 -
Найдите сумму первых 12 членов последовательности, заданной формулой : an=4n-5...
 amaii21.09.2020 19:04
amaii21.09.2020 19:04 -
Вычислить а) sin (-23п/6) б) ctg (-600)...
 erkr29.08.2020 14:22
erkr29.08.2020 14:22 -
Вычислить предел по правилу лопиталя (x^2-16)/(x^2-5x+4)...
 Tomkaya20.12.2021 17:40
Tomkaya20.12.2021 17:40 -
Вычислите координаты точек пересечения графиков уравнения x²+y²=5 и x-y=1...
 Chillin27.04.2023 02:55
Chillin27.04.2023 02:55 -
Выражение : 1+ ctg(p+a) tg (3p/2 - a)...
 zobitkov22.10.2022 03:23
zobitkov22.10.2022 03:23 -
1.розвязати рівняння : 1)(x-2)(x в 2 степені +2x+4)=24x+x в 3 степені 2)(2х+1)...
 Kirill1500316.11.2020 12:29
Kirill1500316.11.2020 12:29 -
Известно, что одно из двух чисел меньше другого на 28. найдите эти числа,...
 dina058511.06.2021 09:07
dina058511.06.2021 09:07 -
Укажите промежуток, содержащий отрицательный корень уравнения: log 6 ( x...
 krasotkinaeliz05.12.2020 13:51
krasotkinaeliz05.12.2020 13:51 -
Укажите 2 соседних числа , между которыми заключено число 3√7 1)3 и 4 2)...
 sasha1175122.03.2021 11:01
sasha1175122.03.2021 11:01