Задача по правилу Лопиталя. Понимаю что нужно записать в качестве натурального логаритма, но получаю бесконечность/0 и немогу применить теорему лопиталя

152

408

Посмотреть ответы 2

Ответы на вопрос:

Даша182005

Математика

4,7(77 оценок)

Пошаговое объяснение:

$\lim _{x \to0} \big((2x)^{tg \: {x}} \big) = \left[ {0}^{0} \right] = \lim _{x \to0} { e}^{ \ln\left((2x)^{tg \: {x}} \right)} = \\ = \lim _{x \to0} { e}^{ tg \: {x} {\cdot}\ln(2x) } = { e}^{\lim _{x \to0} (tg \: {x} {\cdot}\ln(2x)) } = \\$

Здесь ключевой момент!

Мы неопределенность [tg • ln] или [бскнч • 0]

преобразуем по формуле:

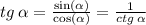
$tg \: \alpha = \frac{ \sin( \alpha ) }{ \cos( \alpha ) } = \frac{1}{ctg \: \alpha } \\$

т.к. функция тангенс это же (1 / котангенс)!

Потом - правило Лопиталя.

$\: = {\lim _{x \to0} (tg \: {x} {\cdot}\ln(2x)) } =\left[ \infty \cdot0 \right] = \\ = {\lim _{x \to0} \frac{\ln2x}{ctg \: {x}} } =\left[ \frac{0}{0} \right] = \lim _{x \to0} \frac{(\ln2x)'}{(ctg \: {x})'} = \\ = \large \lim _{x \to0} \small{\: \frac{ \dfrac{2}{2x} }{- \dfrac{1}{ \sin^{2}x } } } = \large \lim _{x \to0} \small{\: - \frac{2\sin^{2}x}{2x } } = \\ - \lim _{x \to0} \small{\: \frac{\sin^{2}x}{x } } =\left[ \: \frac{0}{0} \: \right] =... \\$

Еще раз правило Лопиталя:

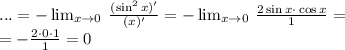
$\\... = - \lim _{x \to0} \small{\: \frac{(\sin^{2}x)'}{(x )'} } =- \lim _{x \to0} \small{\: \frac{2\sin{x}{ \cdot}\cos{x}}{1} } =\\ = - \frac{2 \cdot0 \cdot1}{1} = 0 \\$