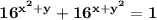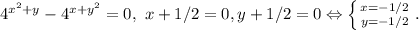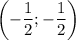Ответы на вопрос:
Объяснение:
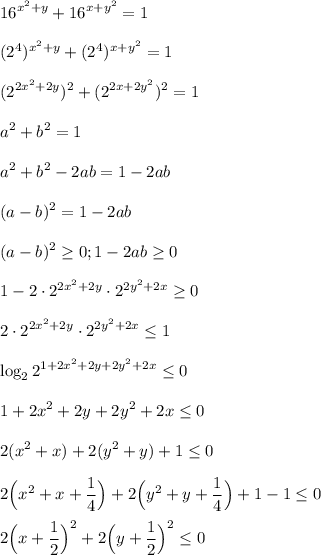
сумма двух неотрицательных слагаемых ≤ 0
возможно только равенство 0 если каждое слагаемое равно 0
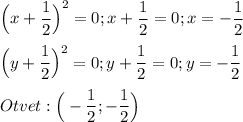
Популярно: Алгебра
-
Выберите из графиков параллельные: y=3x-2 y=2x+1 y=-x+1 y=-2x...
 Yaroslav164028.03.2020 04:49
Yaroslav164028.03.2020 04:49 -
Решите систему уравнения методом подстановки xy=-1 x+2y=1 x^2+xy=6...
 Vania5425.11.2020 13:15
Vania5425.11.2020 13:15 -
Вкаких границах заключена масса m овсяных хлопьев если на упаковке...
 Zaika643202.01.2022 20:59
Zaika643202.01.2022 20:59 -
Разложите выражение на множители: √(x²-y²) + √(x+y)...
 ns15119902.08.2021 19:45
ns15119902.08.2021 19:45 -
Нужно решить и сделать полный анализ. y=4x/(x+1) то что в скобках...
 kitikunit29.12.2021 09:26
kitikunit29.12.2021 09:26 -
Найти производную 1)cos(x^4 +1) 2)tg(x^2 -3x+5) 3) tg(sinx)...
 emma6666920.09.2022 10:59
emma6666920.09.2022 10:59 -
Квадратным корнем из какого числа является число: 1)2 ; 2)7...
 andrey589028.09.2021 05:26
andrey589028.09.2021 05:26 -
Икс в кводрате минус икс больше или равно нулю...
 nikita601123.06.2023 23:25
nikita601123.06.2023 23:25 -
Найдите корень уравнения -3+4 (-7+5x)=9x-9...
 Sagi51118.02.2022 07:43
Sagi51118.02.2022 07:43 -
Принадлежат ли графику функции у=х точка а)а(5; 5) б)с(5; -5)...
 vlerut124.06.2020 17:00
vlerut124.06.2020 17:00