Найти общее решение или общий интеграл дифференциального уравнения.
Решить задачу Коши.

266

296

Посмотреть ответы 2

Ответы на вопрос:

спаситепомогите111

Алгебра

4,4(52 оценок)

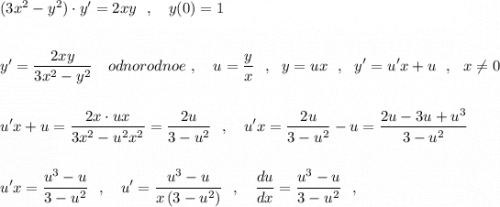
$(3x^2-y^2)\cdot y'=2xy\ \ ,\ \ \ y(0)=1y'=\dfrac{2xy}{3x^2-y^2}\ \ \ odnorodnoe\ ,\ \ \ \displaystyle u=\frac{y}{x}\ \ ,\ \ y=ux\ \ ,\ \ y'=u'x+u\ \ ,\ \ x\ne 0u'x+u=\frac{2x\cdot ux}{3x^2-u^2x^2}=\frac{2u}{3-u^2}\ \ ,\ \ \ u'x=\frac{2u}{3-u^2}-u=\frac{2u-3u+u^3}{3-u^2}u'x=\frac{u^3-u}{3-u^2} \ \ ,\ \ \ u'=\frac{u^3-u}{x\, (3-u^2)}\ \ ,\ \ \ \frac{du}{dx}=\frac{u^3-u}{3-u^2}\ \ ,$

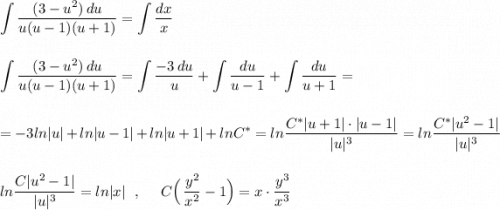
$\displaystyle \int \frac{(3-u^2)\, du}{u(u-1)(u+1)}=\int \frac{dx}{x}int \frac{(3-u^2)\, du}{u(u-1)(u+1)}=\int \frac{-3\, du}{u}+\int \frac{du}{u-1}+\int \frac{du}{u+1}==-3ln|u|+ln|u-1|+ln|u+1|+lnC^*=ln\frac{C^*|u+1|\cdot |u-1|}{|u|^3}=ln\frac{C^*|u^2-1|}{|u|^3}ln\frac{C|u^2-1|}{|u|^3}=ln|x|\ \ ,\ \ \ \ C\Big(\, \frac{y^2}{x^2}-1\Big)=x\cdot \frac{y^3}{x^3}$

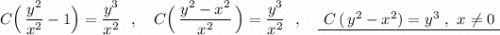
$C\Big(\, \dfrac{y^2}{x^2}-1\Big)=\dfrac{y^3}{x^2}\ \ ,\ \ \ C\Big(\, \dfrac{y^2-x^2}{x^2}\, \Big)=\dfrac{y^3}{x^2}\ \ ,\ \ \ \underline{\ C\, (\, y^2-x^2)=y^3\ ,\ x\ne 0\ }$

Так как получили решение при х≠0 , то найти частное решение при у(0)=1 невозможно .

Например, если бы задали у(1)=2, то

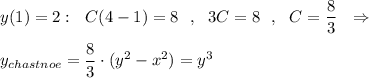
$y(1)=2:\ \ C\codt (4-1)=8\ \ ,\ \ 3C=8\ \ ,\ \ C=\dfrac{8}{3}\ \ \Rightarrow y_{chastnoe}=\dfrac{8}{3}\cdot (y^2-x^2)=y^3$

myisipov1erg

Алгебра

4,7(23 оценок)

Frac{(a+b)^3+(a-b)^3}{2ab(a^2+3b^2)} - 1 frac{(a^2-ab+b^2)(a+b)^2(a-b)}{(a^3+b^3)(a^2-b^2)}=( a^3+3a^2b+3ab^2+b^3 + a^3-3a^2b+3ab^2-b^3) /(2ab(a^2+3b^2)) - 1 == (1-b) / b (a+b)^3+(a-b)^3 / (2ab(a^2+3b^2)) - 1 ==(2a-2ab)(a^2+3b^2) /(2ab(a^2+3b^2)) = (2a-2ab) /(2ab)=2a(1-b)/(2ab)==(2a(a^2+3b^2) -2ab(a^2+3b^2)) /(2ab(a^2+3b^2)) ==(2a^3+6ab^2) /(2ab(a^2+3b^2)) -(2ab(a^2+3b^2)) /(2ab(a^2+3b^2))