Алгебра: 2 X + 6x + 9 X2 + 11x + 24 Сократите дробь,

AlenaStypak

03.12.2021 06:21

Алгебра

Есть ответ 👍

2
X + 6x + 9
X2 + 11x + 24
Сократите дробь,

289

409

Посмотреть ответы 1

Ответы на вопрос:

isaevavika

Алгебра

4,4(71 оценок)

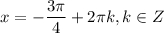
$x=-\dfrac{3\pi}{4}+2\pi k, k\in Z$

Объяснение:

Заметим:

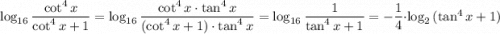
1) $\log_{16}{\dfrac{\cot^4x}{\cot^4x+1}}=\log_{16}{\dfrac{\cot^4x\cdot \tan^4 x}{(\cot^4x+1)\cdot \tan^4 x}}=\log_{16}{\dfrac{1}{\tan^4 x+1}}=-\dfrac{1}{4}\cdot \log_{2}{(\tan^4 x+1)}$

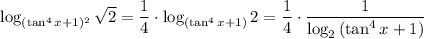
2) $\log_{(\tan^4x+1)^2}\sqrt{2}=\dfrac{1}{4}\cdot \log_{(\tan^4x+1)}2=\dfrac{1}{4}\cdot \dfrac{1}{\log_{2}{(\tan^4 x+1)}}$

Уравнение перепишем в виде

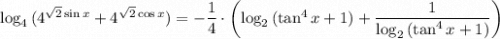$\log_4{(4^{\sqrt{2}\sin x}+4^{\sqrt{2}\cos x})}=-\dfrac{1}{4}\cdot \left(\log_{2}{(\tan^4 x+1)}+\dfrac{1}{\log_{2}{(\tan^4 x+1)}} \right)$ . При этом (основание логарифма не равно 1) 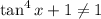$\tan ^4x +1\neq 1$ . Тогда верна цепочка неравенств

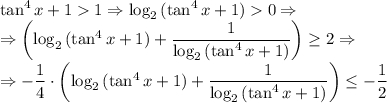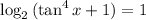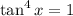$\tan^4 x+1 1\Rightarrow \log_{2}{(\tan^4 x+1)} 0\Rightarrow \\ \Rightarrow\left(\log_{2}{(\tan^4 x+1)}+\dfrac{1}{\log_{2}{(\tan^4 x+1)}} \right) \geq 2\Rightarrow \\ \Rightarrow-\dfrac{1}{4}\cdot \left(\log_{2}{(\tan^4 x+1)}+\dfrac{1}{\log_{2}{(\tan^4 x+1)}} \right) \leq -\dfrac{1}{2}$ , причем равенство может достигаться лишь при $\log_{2}{(\tan^4 x+1)}=1$ , т.е. при $\tan^4 x=1$ .

Оценим теперь левую часть полученного уравнения.

По неравенству о средних верно

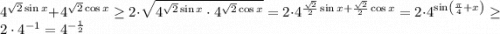
$4^{\sqrt{2}\sin x}+4^{\sqrt{2}\cos x}\geq 2\cdot \sqrt{4^{\sqrt{2}\sin x}\cdot 4^{\sqrt{2}\cos x}}=2\cdot 4^{\frac{\sqrt{2}}{2}\sin x+\frac{\sqrt{2}}{{2}}\cos x}=2\cdot 4^{\sin\left(\frac{\pi}{4}+x\right)}\geq 2\cdot 4^{-1}=4^{-\frac{1}{2}}$

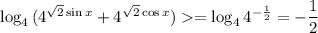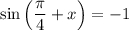Отсюда (т.к. основание 4 логарифма больше 1) верна оценка $\log_4{(4^{\sqrt{2}\sin x}+4^{\sqrt{2}\cos x})} =\log_4{4^{-\frac{1}{2}}}=-\dfrac{1}{2}$ , причем равенство может достигаться лишь при $\sin\left(\dfrac{\pi}{4}+x\right)=-1$ .

Значит, решение уравнения эквивалентно решению системы

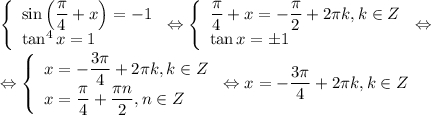
$\left\{\begin{array}{l}\sin\left(\dfrac{\pi}{4}+x\right)=-1\\\tan^4 x=1\end{array}\right.\Leftrightarrow \left\{\begin{array}{l}\dfrac{\pi}{4}+x=-\dfrac{\pi}{2}+2\pi k, k\in Z\\\tan x=\pm1\end{array}\right.\Leftrightarrow \\\Leftrightarrow\left\{\begin{array}{l}x=-\dfrac{3\pi}{4}+2\pi k, k\in Z\\x=\dfrac{\pi}{4}+\dfrac{\pi n}{2}, n\in Z\end{array}\right.\Leftrightarrow x=-\dfrac{3\pi}{4}+2\pi k, k\in Z$