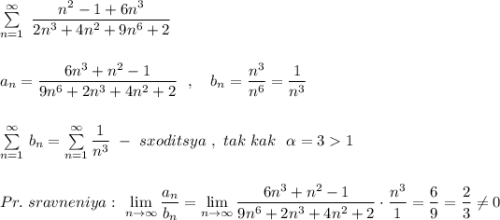Ответы на вопрос:
Популярно: Алгебра
-
Запишіть будь яка систему рівнянь що має розв язок( -2;5)...
 Mamishbdjsnb24.05.2021 08:02
Mamishbdjsnb24.05.2021 08:02 -
4.2. Користуючись таблицею розвитку Київського метрополітену, добудуйте...
 00909524455445817.03.2021 19:35
00909524455445817.03.2021 19:35 -
Напишите уравнение касательной к графику функции x^3 + x^2 в точке...
 Zoomf04.10.2021 19:36
Zoomf04.10.2021 19:36 -
Упрастите выражение (39.8-39.9) :12-3х/х-2+10-х/2-х...
 Йфяалмглиоаиопр25.10.2020 04:54
Йфяалмглиоаиопр25.10.2020 04:54 -
(8−y)2−y(y+6), если y=210...
 sot5806.09.2022 01:02
sot5806.09.2022 01:02 -
побудуйте график функции y=3х-2 користуючись графиком знайдить значение...
 Versysbatl14.07.2022 15:18
Versysbatl14.07.2022 15:18 -
каково примерное расположение графика функции y=kx+l если 1)k 0,l...
 svyatkin11120.09.2022 14:43
svyatkin11120.09.2022 14:43 -
. Очень нужно (1/4)^2/3 27 4/3 (4/9)^3/4 Х^0,2х^-1х^0,6 а^2/3a^1/6a5/3...
 Липапит29.03.2023 13:01
Липапит29.03.2023 13:01 -
Два каменщика укладывают плиткой два одинаковых участка мостовой,...
 списыватель14706.04.2020 13:57
списыватель14706.04.2020 13:57 -
X- в 6 степени умножить на x-в 4 степени, деленное на x²...
 дарья162722.05.2020 22:00
дарья162722.05.2020 22:00