пример 2 и 4. Все теоремы и аксиомы, будьте добры, распишите. Действий, пусть и банальных, легких не упускайте. Распишите полностью.
Ответы на вопрос:
По определению, 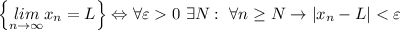
Т.к. в обоих случаях нужно обосновать, что L=0, определение преобразуется в утверждение 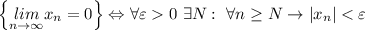
2) 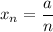
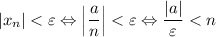
А значит, если взять ![N=\left[\dfrac{|a|}{\varepsilon}\right] +1](/tpl/images/3820/0626/0d89e.png) (*),
(*), 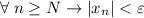 . И правда:
. И правда: 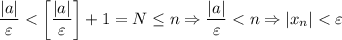
(*) Очевидно, что для любого допустимого значения  выражение
выражение ![\left[\dfrac{|a|}{\varepsilon}\right] +1](/tpl/images/3820/0626/ae843.png) определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (*)
определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (*)
А это и означает, что предел данной последовательности равен 0
4) 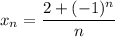
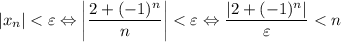
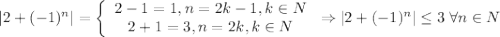
А значит, если взять ![N=\left[\dfrac{3}{\varepsilon}\right] +1](/tpl/images/3820/0626/a4ca4.png) (**),
(**), 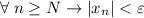 . И правда:
. И правда: ![\dfrac{|2+(-1)^n|}{\varepsilon}\leq\dfrac{3}{\varepsilon}< \left[\dfrac{3}{\varepsilon}\right] +1=N\leq n \Rightarrow \dfrac{|2+(-1)^n|}{\varepsilon}< n \Rightarrow |x_n|](/tpl/images/3820/0626/49458.png)
(**) Очевидно, что для любого допустимого значения  выражение
выражение ![\left[\dfrac{3}{\varepsilon}\right] +1](/tpl/images/3820/0626/698f8.png) определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (**)
определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (**)
А это и означает, что предел данной последовательности равен 0
___________________________
2) a=1. Тогда 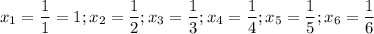
4)
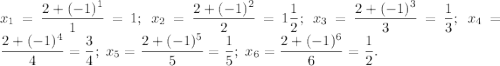
___________________________
Обозначения и некоторые св-ва: {x} - дробная часть числа x, [x] - целая часть числа x. 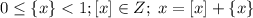
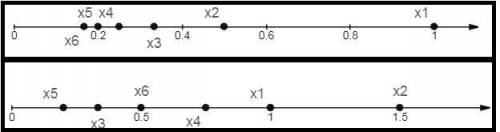
(см. объяснение)
Объяснение:
Попробуем доказать равенство:
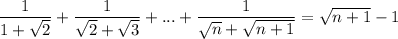
Применим метод математической индукции.
Докажем базу индукции для 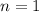 :
:
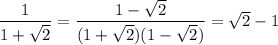 , верно.
, верно.
Докажем переход:
Предположим, что для 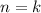 выполнено:
выполнено:
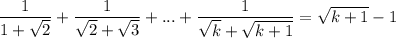
Тогда для 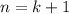 согласно предположению:
согласно предположению:
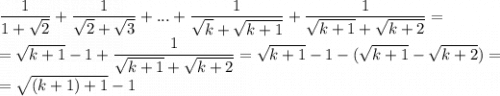
Значит по принципу математической индукции равенство выполнено для всякого 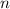 .
.
Наконец, получили, что:
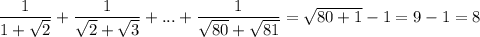
Из данных рассуждений заключаем, что правильный ответ указан под буквой Г.
Задание выполнено!
Популярно: Алгебра
-
2cos^2 x-5cos(-3п/2-x)+1=0 решить уравнение...
 отличница5457517.09.2022 20:41
отличница5457517.09.2022 20:41 -
Решить уравнение: -5x²-9x=0 2x²+3x=0...
 алинка55424.07.2022 03:40
алинка55424.07.2022 03:40 -
Родительский комитет закупил 10 пазлов для подарков детям к окончанию года,из них...
 Yuiyuii16.10.2020 22:00
Yuiyuii16.10.2020 22:00 -
Призерами городской олимпиады по стало 24 ученика, что составило 15% от числа участников....
 girlssss03.02.2022 10:53
girlssss03.02.2022 10:53 -
Найдите корень уравнения 2 в степени(9+х)=8...
 1994242401.04.2020 03:37
1994242401.04.2020 03:37 -
Пять одинаковых тетрадей толще чем общая тетрадь на 16%. на сколько процентов восемь...
 fedya3301.02.2020 23:00
fedya3301.02.2020 23:00 -
5b^3-3b^5 xa-5c+5a-xc 3a^4-48b^4 -4x^2+24x-36 разложить на множители...
 СофариПарк327.11.2020 16:33
СофариПарк327.11.2020 16:33 -
Найдите значение выражения: 49^2⋅4^3: 196....
 Nadia356721.03.2020 14:14
Nadia356721.03.2020 14:14 -
Найдите значения производной в точке x; 0 f(x)=(2x^2-3x+1) x o=1...
 Nicol0324.06.2023 07:10
Nicol0324.06.2023 07:10 -
Найти значение выражения: логарифм 45 по основанию 6-логарифм 7,5 по основанию...
 Поли32210.12.2022 23:22
Поли32210.12.2022 23:22
