Регистрация
mayakmaria
06.02.2023 20:17
Математика
Есть ответ 👍

Доказать, что для всех натуральных n верно неравенство:

198
272
Посмотреть ответы 2

Ответы на вопрос:

kotovaalina31
kotovaalina31
4,6(22 оценок)

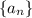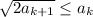Пусть последовательность \{a_{n}\} такова, что для всех k\geq m выполнено неравенство \sqrt{2a_{k+1}}\leq a_{k. Тогда верно неравенство 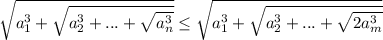\sqrt{a_{1}^3+\sqrt{a_{2}^3+...+\sqrt{a_{n}^3}}}\leq \sqrt{a_{1}^3+\sqrt{a_{2}^3+...+\sqrt{2a_{m}^3}}}.  Это легко видеть, заменяя члены с использованием неравенства.

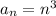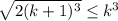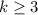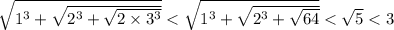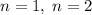В нашем случае a_{n}=n^3, неравенство \sqrt{2(k+1)^3}\leq k^3 верно для всех натуральных k\geq 3. Значит, искомая сумма не превосходит \sqrt{1^3+\sqrt{2^3+\sqrt{2\times3^3}}}. Для n=1,\; n=2 очевидно.

jjiki
jjiki
4,4(87 оценок)

ответ: 6кг.

пошаговое объяснение:

х один арбуз ; х/2 половина арбуза.

х+х/2=9;

1,5х=9;

х-9/1,5=6 кг весит один арбуз.

Популярно: Математика