Регистрация
diman211102
05.06.2022 15:26
Математика
Есть ответ 👍

Найдите объем тела, заданного ограничивающими его поверхностями

237
458
Посмотреть ответы 2

Ответы на вопрос:

Настя200101
Настя200101
4,7(64 оценок)

Пошаговое объяснение:

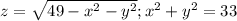
z= \sqrt{49-x^{2}-y^2 } ; x^{2} +y^2 = 33

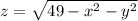z= \sqrt{49-x^{2}-y^2 } - это верхняя половина сферы с радиусом 7 и центром в начале координат

х² + у² = 33 - это цилиндр с осью по OZ радиусом r = √33

рисунок прилагается

найдем пересечение этих фигур

z = √(49-33) = √16 = 4

V = ∫∫∫dx dy dz

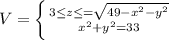
V = \left \{ {{3\leq z\leq =\sqrt{49-x^{2}-y^2 } } \atop {x^2+y^2=33}} \right.

перейдем к цилиндрическим координатам

\left[\begin{array}{ccc}r cos\alpha\\y= r sin\alpha ;dxdydz=rdrd\\ z=z\end{array}\right]

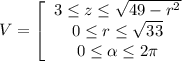
V = \left[\begin{array}{ccc}{3\leq z \leq \sqrt{49-r^2}\\{0\leq r\leq \sqrt{33} \\0\leq \alpha \leq 2\pi \end{array}\\

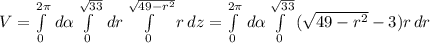
V=\int\limits^{2\pi }_0 {} \, d\alpha \int\limits^{\sqrt{33}} _0 {} \, dr \int\limits^{\sqrt{49-r^2} }_0 {r} \, dz =\int\limits^{2\pi }_0 {} \, d\alpha \int\limits^{\sqrt{33}} _0 {(\sqrt{49-r^2}-3})r \, dr

посчитаем

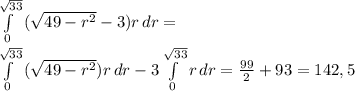
\int\limits^{\sqrt{33}} _0 {(\sqrt{49-r^2}-3})r \, dr =\\ \int\limits^{\sqrt{33}} _0 {(\sqrt{49-r^2}})r \, dr -3\int\limits^{\sqrt{33}} _0 r \, dr =\frac{99}{2}+93 = 142,5

теперь, наконец, посчитаем объем

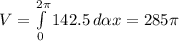
V = \int\limits^{2\pi }_0 {142.5} \, d\alpha x = 285\pi

           

marschmello
marschmello
4,4(51 оценок)

30. сторінок

Пошаговое объяснение:

100%-88%=12%

3.6-12%

х - 100%

х - весь текст

х=100*3.6/12=360/12=30

Популярно: Математика