МАКСИМУМ БАЛЛОВ С пояснениями и оформлением(найти и дано, чертеж)
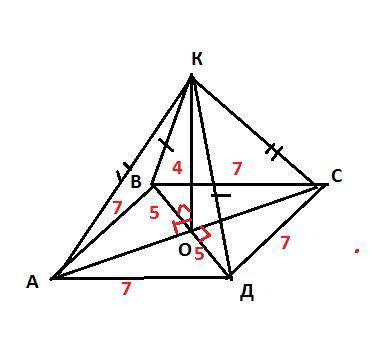
Длина стороны ромба АВСД равна 7 см, длина диагонали ВД= 10 см. Через
точку О пересечения диагоналей ромба проведена прямая ОК,
перпендикулярная его плоскости. Найти расстояние от точки К до вершин
ромба, если ОК= 4 см.
159
335
Ответы на вопрос:
ответ: 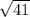 см, 2
см, 2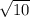 см
см
Объяснение: Смотрите рисунок
ВО = 10/2=5 см - это половина диагонали.
В прямоугольном треугольнике ВОМ по Пифагору, расстояние от точки К до вершин В и Д будет
ВK^2 = 5^2+4^2 = 25+16 = 41
Тогда ВК=КД = 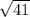 см
см
Найдем АО. Диагонали ромба перпендикулярны, поэтому треугольник АОВ прямоугольный и сторона = 7 см - гипотенуза.
По Пифагору AO^2 = 7^2 - 5^2 = 49 -25 = 24
расстояние от точки К до точек А и С будет
АК^2 = AO^2 + OK^2 = 24 + 16 = 40
Тогда АК = СК = 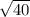 = 2
= 2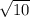 см
см
sin^2 a+cos^2 a = 1 ( основное тригонометрическое свойство)
sin a =
sin a = /10
sin a = ch/ac
ch = ac*sin a
ch = (6*)/5
Популярно: Геометрия
-
Дано вибірку 5;9;7;3. знайдіть а) розмах вибірки б) середнє значення...
 AnikaNay09.12.2021 22:41
AnikaNay09.12.2021 22:41 -
найти площадь трапеции найти площадь трапеции...
 mistermelya21.03.2022 14:36
mistermelya21.03.2022 14:36 -
Сторона квадрата дорівнює 9 см. Знайти діагональ квадрата....
 prooverrseer17.06.2021 18:27
prooverrseer17.06.2021 18:27 -
Знайдіть відношення площ двох квадратів, якщо їхні сторони дорівнюють 1)2 см і...
 blackcat1827.04.2023 09:06
blackcat1827.04.2023 09:06 -
всей душой у меня жопа всей душой у меня жопа >...
 20Sascha0723.09.2022 06:18
20Sascha0723.09.2022 06:18 -
Один із суміжних кутів на 14 градусів більший за другий. Яка градусна міра менша...
 BPAN32131.07.2021 17:57
BPAN32131.07.2021 17:57 -
Точка С делит отрезок АВ = 30 см на два отрезка. АС больше СВ в 5 раз. Тогда длина...
 ваня32323223304.09.2022 04:41
ваня32323223304.09.2022 04:41 -
Сторона ромба дорівнює 6 см, гострий кут 60° . Діагоналі ромба дорівнюють.... 1...
 Дианп1113.03.2020 08:31
Дианп1113.03.2020 08:31 -
Сторона шестикутника вписаного в коло з радіусом 8 см дорівнює......
 умник20061010.02.2021 23:11
умник20061010.02.2021 23:11 -
Напишиье сочинение на тему Мои любимые компьютерные программы...
 sabinabaigali28.01.2021 11:15
sabinabaigali28.01.2021 11:15
