Нужна ! даны точки а(0; -3; 6) b(-12; -3; -3) c(-9; -3; -6). найти длины векторов ав и ас ; их скалярное произведение ав * ас и угол между ними.
271
366
Ответы на вопрос:
ОДЗ:
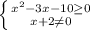
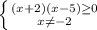
x∈(-∞; -2) U [5;+∞)
Решаем на каждом промежутке:
На [5:+∞)
(x+2) >0 ⇒ умножаем обе части неравенства на (х+2).
Знак неравенства при этом не меняется
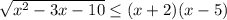
Замена переменной:
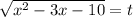 ⇒
⇒ 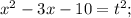
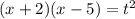
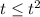
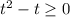
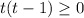
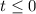 или
или 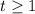
Обратная замена:
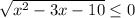 или
или 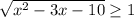
x=-2 или x=5 или 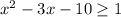 ⇒
⇒ 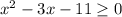
. или D=9+44=53; 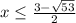 или
или 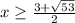
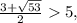 так как
так как 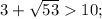 а
а 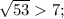
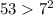
c учетом x∈ [5:+∞) и 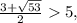
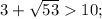 а
а 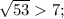
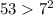
получаем о т в е т. 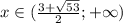
На (-∞;- 2)
(x+2) <0 ⇒ умножаем обе части неравенства на (х+2).
Знак неравенства при этом меняется
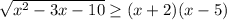 Та же замена.
Та же замена.
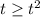 ⇒
⇒ 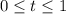 ⇒
⇒ 
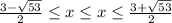
c учетом x∈ (-∞; -2) и 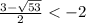 ⇒
⇒ 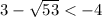 ;
; 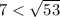
получаем о т в е т. 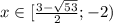
Объединяем ответы двух рассмотренных случаев:
 - О т в е т.
- О т в е т.
Популярно: Математика
-
Задуманное число было увеличено в 4 раза.полученное значение произведения...
 Verrunnya10.01.2023 02:02
Verrunnya10.01.2023 02:02 -
Мама поручила саше купить картошку. килограмм стоит 63 р. какое наибольшее...
 ssssss213r53219.04.2022 16:14
ssssss213r53219.04.2022 16:14 -
Сто депутатов образовали 450 комиссий.каждые две комиссии пересекаются...
 alyasen200601.06.2020 20:27
alyasen200601.06.2020 20:27 -
Запиши и прочитай числа, которые разложены в виде суммы разрядных слогаемых....
 chhfyf03.11.2021 01:56
chhfyf03.11.2021 01:56 -
Решите уравнения (2x+3)^2-7=(2-1)(2x+1)...
 stazagreen17.04.2020 12:04
stazagreen17.04.2020 12:04 -
Представьте в виде обыкновенной дроби числа: 0,5 ; 0,16 ; 0,25 люди я...
 Вовка75316.06.2021 20:31
Вовка75316.06.2021 20:31 -
Начало прочитайте число *3 : 20 меньше 12? да *100 нет *10 запишите результат...
 vladyslav252330.03.2020 05:07
vladyslav252330.03.2020 05:07 -
Построй ломаную из двух звеньев.длина одного звена 3 см 9 мм а другого...
 varvara27326.08.2021 13:36
varvara27326.08.2021 13:36 -
Надо написать реферат на тему лёгкая атлетика....
 Pharaonua07.08.2021 05:15
Pharaonua07.08.2021 05:15 -
Периметр квадрата, равен периметру прямоугольника. площадь квадрата равна...
 Frog77728.07.2022 13:38
Frog77728.07.2022 13:38
