Регистрация
аліна55
11.07.2020 19:52
Алгебра
Есть ответ 👍

Решите уравнение(x^2+4x)(x^2+4x-17)+60=0

288
440
Посмотреть ответы 2

Ответы на вопрос:

Dimamysixin
Dimamysixin
4,8(7 оценок)
Пусть   t=x²+4x t(t-17)+60=0 t²-17t+60=0 d= (-17)² -4*60=289-240=49=7² t₁=(17-7)/2=10/2=5 t₂=(17+7)/2=12 при t=5 x²+4x=5 x²+4x-5=0 d=4² -4*(-5)=16+20=36=6² x₁=(-4-6)/2= -10/2= -5 x₂=(-4+6)/2=1 при t=12 x²+4x=12 x²+4x-12=0 d=4² -4*(-12)=16+48=64=8² x₁=(-4-8)/2=-12/2= -6 x₂=(-4+8)/2=4/2=2 ответ: -6;   -5;   1;   2.
Mariya1616161
Mariya1616161
4,7(48 оценок)

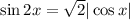
\sin2x=\sqrt{2} |\cos x|

1. Раскроем модуль при условии 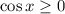\cos x\geq 0:

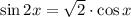
\sin2x=\sqrt{2} \cdot\cos x

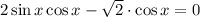
2\sin x\cos x-\sqrt{2} \cdot\cos x=0

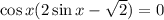
\cos x(2\sin x-\sqrt{2}) =0

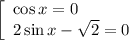
\left[\begin{array}{l} \cos x=0\\ 2\sin x-\sqrt{2} =0\end{array}

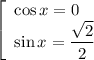
\left[\begin{array}{l} \cos x=0\\ \sin x=\dfrac{\sqrt{2} }{2}\end{array}

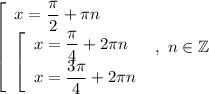
\left[\begin{array}{l} x=\dfrac{\pi}{2}+\pi n \\ \left[\begin{array}{l} x=\dfrac{\pi }{4}+2\pi n \\ x=\dfrac{3\pi }{4}+2\pi n \end{array}\end{array},\ n\in\mathbb{Z}

Однако корни 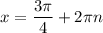x=\dfrac{3\pi }{4}+2\pi n не удовлетворяют условию раскрытия модуля. Поэтому окончательный ответ:

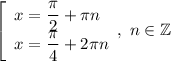
\left[\begin{array}{l} x=\dfrac{\pi}{2}+\pi n \\x=\dfrac{\pi }{4}+2\pi n \end{array},\ n\in\mathbb{Z}

2. Раскроем модуль при условии 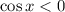\cos x<0:

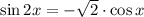
\sin2x=-\sqrt{2} \cdot\cos x

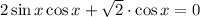
2\sin x\cos x+\sqrt{2} \cdot\cos x=0

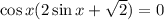
\cos x(2\sin x+\sqrt{2} )=0

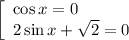
\left[\begin{array}{l} \cos x=0\\ 2\sin x+\sqrt{2} =0\end{array}

Заметим, что первое уравнение не удовлетворят условию раскрытия модуля. Продолжаем решать только второе уравнение:

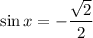
\sin x=-\dfrac{\sqrt{2} }{2}

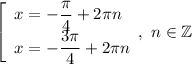
\left[\begin{array}{l} x=-\dfrac{\pi }{4}+2\pi n \\ x=-\dfrac{3\pi }{4}+2\pi n \end{array},\ n\in\mathbb{Z}

Однако корни 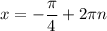x=-\dfrac{\pi }{4}+2\pi n не удовлетворяют условию раскрытия модуля. Поэтому окончательный ответ этого случая:

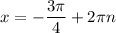
x=-\dfrac{3\pi }{4}+2\pi n

3. Объединим решения, полученные в предыдущих пунктах:

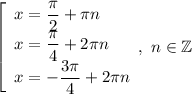
\left[\begin{array}{l} x=\dfrac{\pi}{2}+\pi n \\x=\dfrac{\pi }{4}+2\pi n\\ x=-\dfrac{3\pi }{4}+2\pi n \end{array},\ n\in\mathbb{Z}

Или более кратко:

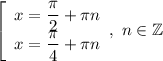
\left[\begin{array}{l} x=\dfrac{\pi}{2}+\pi n \\x=\dfrac{\pi }{4}+\pi n \end{array},\ n\in\mathbb{Z}

ответ: 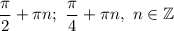\dfrac{\pi}{2}+\pi n;\ \dfrac{\pi }{4}+\pi n,\ n\in\mathbb{Z}

Популярно: Алгебра